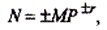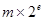выражение одного типа данных через данные другого типа это

Рис. 5. Вещественное число с плавающей точкой.

Количество позиций, отводимых для мантиссы, определяет точность представления чисел, а количество позиций, отводимых для порядка – диапазон представления чисел.

Обычно мантисса записывается в нормализованном виде, то есть так, чтобы отсутствовали незначащие нули в старших разрядах:

0.0011101 ненормализованное представление,

0.1110100 нормализованное представление.

При сложении чисел в форме с плавающей точкой в общем случае нельзя складывать их мантиссы. Если слагаемые имеют разные порядки, то одинаковые разряды мантиссы будут на самом деле изображать разные разряды числа. Поэтому при сложении чисел необходимо предварительно выровнять их порядки, то есть числу с меньшим порядком приписать порядок второго числа и соответствующим образом изменить мантиссу

2.4. Кодирование текстовых данных

Если каждому символу алфавита сопоставить целое число, то можно с помощью двоичного кода кодировать текстовые данные. Восьми двоичных разрядов достаточно для кодирования 256 различных символов. Этого хватает, чтобы закодировать все строчные и прописные буквы английского или русского алфавита, а также знаки препинания, цифры, символы основных арифметических операций и некоторые специальные символы, например «%».

Технически это просто, но существуют организационные сложности. Для того чтобы весь мир одинаково кодировал текстовые данные, нужны единые таблицы кодирования, а это трудно осуществить из-за использования различных символов в национальных алфавитах. Сейчас по ряду причин наибольшее распространение получил стандарт США ANСII (American National Code for Information Interchange) – Американский национальный код для обмена информацией. В системе кодирования ANСII закреплены две таблицы кодирования: базовая со значениями кодов от 0 до 127 и расширенная с кодами от 128 до 255.

Коды от 0 до 31 базовой таблицы содержат так называемые управляющие коды, которым не соответствуют символы языка. Они служат для управления устройствами ввода-вывода. Коды с 32 по 127 служат для кодирования символов английского алфавита, знаков препинания, цифр и некоторых других символов. Расширенная таблица с кодами от 128 до 255 содержит набор специальных символов.

Аналогичные системы кодирования разработаны и в других странах. В России большое распространение имеет код КОИ-8.

Трудности создания единой системы кодирования текстовых данных связаны с ограниченным набором кодов (256). Если кодировать символы не 8-разрядными двоичными числами, а 16-разрядными, это позволит иметь набор из 65 536 различных кодов. Этого достаточно, чтобы в одной таблице разместить символы большинства языков. Такая система кодирования называется Unicode – универсальный код. Переход к этой системе долго сдерживался из-за недостатка памяти компьютеров, так как в системе Unicode все текстовые документы становятся вдвое длиннее. В настоящее время технические сложности преодолены и происходит постепенный переход на универсальную систему кодирования.

2.5. Кодирование графических данных

Общепринятым сегодня считается представление черно-белых иллюстраций в виде комбинации точек с 256 градациями серого цвета. При этом для кодирования яркости любой точки достаточно 8-разрядного двоичного числа.

Для кодирования цветных графических изображений применяется принцип декомпозиции произвольного цвета на три основных – красный, зелёный и синий. Для кодирования яркости каждой составляющей используется 256 значений (8 двоичных разрядов). Для кодирования цвета используются 24 разряда. Такая система кодирования обеспечивает представление 16,5 млн различных цветов.

Источник

Кодирование информации. Кодирование-это выражение данных одного типа через данные другого типа

Кодирование-это выражение данных одного типа через данные другого типа.

· азбуки – кодирование компонентов языка с помощью графических символов;

· морская флажковая азбука;

· телеграфная азбука и т.д.

Код строится на базе алфавита, состоящего из букв, цифр и других символов. Код характеризуется:

· длиной – число позиций в коде;

· структурой – порядок расположения в коде символов, используемых для обозначения классификационного признака.

Процедура присвоения объекту кодового обозначения называется кодированием.

Способ кодирования чисел называется системой счисления (СС). Система счисления– это способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения Системы счисления (СС) делятся на позиционные и непозиционные.

В позиционных системах счисления количественное значение каждой цифры зависит от ее места в числе.

Если Р- основание системы счисления, т.е. количество используемых цифр, то значения цифр в записи числа лежат в пределах от 0 до Р-1.. В общем случае запись любого смешанного числа в системе счисления с основанием Р будет представлять собой ряд вида:

где нижние индексы определяют местоположение цифры в числе (разряд):

§ положительные значения индексов – для целой части числа (т разрядов);

§ отрицательные значения – для дробной (s разрядов),

В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе. Пользуемся позиционной СС-десятичной. Римская СС – непозиционная, т.е. каждый символ обозначает всегда одно и тоже число; Цифры обозначаются латинскими буквами:

(1, 5, 10, 50, 100, 500, 1000)

В вычислительных машинах применяются две формы представления двоичных чисел:

§ естественная форма или форма с фиксированной запятой (точкой);

§ нормальная форма или форма с плавающей запятой (точкой).

С фиксированной запятой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.

В десятичной системе счисления имеются 5 разрядов в целой части числа (до запятой) и 5 разрядов в дробной части числа (после запятой); числа, записанные в такую разрядную сетку, имеют вид:

Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому не всегда приемлема при вычислениях.

С плавающей запятой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая – порядком, причем абсолютная величина мантиссы должна быть меньше 1, а порядок – целым числом. В общем виде число в форме с плавающей запятой может быть представлено так:

где М – мантисса числа

r – порядок числа ( r – целое число);

Р – основание системы счисления.

Алгоритм перевода чисел из десятичной системы счисления в систему с основанием Р>1.:

1) если переводится целая часть числа, то она делится на Р, после чего запоминается остаток от деления. Полученное частное вновь делится на Р, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным

нулю. Остатки от деления на Р выписываются в порядке, обратном их получению;

2) если переводится дробная часть числа, то она умножается на Р, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на Р и т.д. Процедура продолжается до тех пор, пока дробная часть не

станет равной нулю. Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием Р.

Десятичнаясистема счисления

• Основание системы – число 10;

• Содержит 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;

• Любое десятичное число можно представить в виде суммы степеней числа 10 – основания системы;

Двоичнаясистема счисления имеет основание Р=2 и использует для представления информации всего две цифры: 0 и 1.

• Основание системы – 2;

• Содержит 2 цифры: 0; 1;

• Любое двоичное число можно представить в виде суммы степеней числа 2 – основания системы;

• Примеры двоичных чисел: 11100101; 10101;

1. Пправило перехода из десятичной СС в двоичную СС:

• Разделить десятичное число на 2. Получится частное и остаток.

• Частное опять разделить на 2. Получится частное и остаток.

• Выполнять деление до тех пор, пока последнее частное не станет меньшим 2.

• Записать последнее частное и все остатки в обратном порядке. Полученное число и будет двоичной записью исходного десятичного числа.

Пример.

Задание № 1:

Перевести данное число из десятичной системы счисления в двоичную

(получить пять знаков после запятой в двоичном представлении).

а) 341; 125; 1024; 4095; б) 380,1875(10).

Правило перехода из двоичной системы счисления в десятичную.

Для перехода из двоичной системы счисления в десятичную необходимо двоичное число представить в виде суммы степеней двойки и найти ее десятичное значение.

Двоичные числа 1011001, 11110, 11011011 перевести в десятичную систему.

Восьмеричная СС

• Основание системы – 8;

• Содержит 8 цифры: 0; 1; 2; 3; 4; 5; 6; 7;

• Любое восьмеричное число можно представить в виде суммы степеней числа 8 – основания системы;

• Примеры восьмеричных чисел: 2105; 73461;

Правило перехода из десятичной системы счисления в восьмеричную

• Разделить десятичное число на 8. Получится частное и остаток.

• Частное опять разделить на 8. Получится частное и остаток.

• Выполнять деление до тех пор, пока последнее частное не станет меньшим 8.

• Записать последнее частное и все остатки в обратном порядке. Полученное число и будет восьмеричной записью исходного десятичного числа.

Десятичные числа 421, 5473, 1061 перевести в восьмеричную систему.

Правило перехода из восьмеричной системы счисления в десятичную.

Для перехода из восьмеричной системы счисления в десятичную необходимо восьмеричное число представить в виде суммы степеней восьмерки и найти ее десятичное значение.

Восьмеричные числа 41, 520, 306 перевести в десятичную систему

При программировании иногда используется шестнадцатеричная система счисления, перевод чисел из которой в двоичную систему счисления весьма прост – выполняется поразрядно (полностью аналогично переводу из двоично-десятичной системы). Для изображения цифр, больших 9, в шестнадцатеричной системе счисления применяются буквы А = 10, В = 11, С = 12, D = 13, Е = 14, F = 15.

• Основание системы – 16;

• Содержит 16 цифр: от 0 до 9; A; B; C; D; E; F;

• Любое шестнадцатеричное число можно представить в виде суммы степеней числа 16 – основания системы;

• Примеры шестнадцатеричных чисел: 21AF3; B09D;

Источник

Операции над данными

В структуре возможных операций с данными можно выделить следующие основные понятия:

1. Сбор данных – накопление данных с целью обеспечения достаточной полноты информации для принятия решений;

2. Формализация данных – приведение данных, поступивших из разных источников, к одинаковой форме, чтобы сделать их сопоставимыми между собой, т.е. повысить уровень доступности;

3. Фильтрация данных – отсеивание «лишних» данных, в которых нет необходимости для принятия решений; при этом должен уменьшить уровень «шума», а достоверность и адекватность должны возрастать;

4. Сортировка данных – упорядочение данных по заданному признаку с целью удобства использования;

5. Группировка данных – объединение данных по заданному признаку с целью повышения удобства использования

6. Архивация данных – организация хранения данных в удобной и легкодоступной форме; служит для снижения экономических затрат;

7. Защита данных – это комплекс мер, направленных на предотвращение утраты, воспроизведения и модификации данных;

8. Транспортировка данных (источник данных – сервер, а потребитель – клиент)

9. Преобразование данных – перевод из одной формы в другую.

2. Кодирование данных.

Для автоматизации работы с данными различного типа используется кодирование. Кодирование – это выражение данных одного типа через данные другого типа.

В вычислительной системе используется двоичное кодирование, т. е. представление данных последовательностью всего двух символов 0 и 1.

Целые числа кодируются двоичным кодом достаточно просто. Для кодирования действительных чисел используется 80-разрядное кодирование. При этом число предварительно преобразуется в нормализованную форму.

R =

Первая часть m называется мантиссой, а вторая e – экспонентой. Большая часть бит отводиться для хранения мантиссы (вместе со знаком), и некоторое фиксированное количество для хранения экспоненты.

Для кодирования текстовых данных каждому символу сопоставляется целое число. С помощью восьми двоичных разрядов можно закодировать 256 различных символов. Этого достаточно для кодировки символов английского и русского языков, как строчных, так и прописных, а также знаков препинания, символов арифметических операций и некоторых общепринятых специальных символов.

Институт стандартизации США ввел в действие систему кодирования ASCII (American Standard Code for Information Interchange). В системе ASCII закреплены две таблицы кодирования – базовая и расширенная. Базовая таблица закрепляет значения кодов от 0 до 127, а расширенная относится к символам с номерами от 128 до 255.

Другая система, основанная на 16-разрядном кодировании, является универсальной и называется UNICODE. Шестнадцать разрядов позволяют кодировать до 65 536 различных символов, что достаточно для размещения в одной таблице символом большинства языков планеты.

Любое графическое изображение представляет собой совокупность точек, имеющих различные цвета. Для представления изображения также используется двоичное кодирование, так как линейные координаты и индивидуальные свойства каждой точки можно выразить с помощью целых чисел.

Для кодирования звуковых данных используется FM метод, основанный на том, что теоретически любой сложный звук можно разложить на последовательность простейших гармонических сигналов разных частот. каждый из таких сигналов представляет собой правильную синусоиду, а следовательно может быть числовыми параметрами, т. е. кодом.

3. Основные структуры данных.

Работа с большими наборами данных автоматизируется проще, когда данные упорядочены, т. е. образуют заданную структуру. Структурирование – это введение соглашений о способах представления данных.

Существует три основных типа структур данных: линейная, иерархическая и табличная.

Линейные структуры – это списки. Список – это простейшая структура данных, отличающихся тем, что адрес каждого элемента данных определяется его номером. Обычный журнал посещаемости занятий имеет структуру списка, поскольку студенты зарегистрированы в нем под своими уникальными номерами.

Табличные структуры отличаются от списочных тем, что элементы данных определяются адресом ячейки, который состоит не из одного параметра как в списках, а из нескольких.

Реляционная модель ориентированна на организацию данных в виде двумерных таблиц. Каждая реляционная таблица представляет собой двумерный массив. Отношения представлены в виде таблиц, строки которых соответствуют записям, а столбцы полям.

Содержит перечень объектов одного типа. А каждой строке таблицы последовательно размещаются значение свойств одного из объектов; каждое значение свойства – в своем столбце, озаглавленное именем свойства.

Поле, каждое значение которого однозначно определяет соответствующую запись, называется простым ключом или ключевым полем.

Система управления базами данных (СУБД) – программа, которая позволяет создавать базы данных и обеспечивает обработку, сортировку и поиск данных.

Окно базы данных – один из главных элементов Access. В нем представлены все объекты БД.

Таблицы – базовый объект БД. Все остальные объекты создаются на основе таблиц. Столбцы в такой таблице называют полями, строки – записями.

Запросы – являются основным инструментом БД. С их помощью осуществляется отбор данных, исходя из заданных условий;

Отчеты – предназначены для печати данных, выбранных согласно запросу;

Формы – позволяют добавлять в таблицы новые данные, корректировать существующие. Форма может содержать графики, рисунки и другие внедренные объекты;

Макросы – как и в других приложениях, служат для автоматизации часто повторяющихся операций.

Источник