Свойства степени
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
Данное свойство степеней также действует на произведение трёх и более степеней.
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:

Свойства 4
Степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4
Свойства 5
Степень частного (дроби)
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Свойства степеней: формулировки, доказательства, примеры
Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.
Свойства степени с натуральным показателем
1. Главное свойство степени: a m · a n = a m + n
2. Свойство частного для степеней, имеющих одинаковые основания: a m : a n = a m − n
3. Свойство степени произведения: ( a · b ) n = a n · b n
Равенство можно расширить до: ( a 1 · a 2 · … · a k ) n = a 1 n · a 2 n · … · a k n
4. Свойство частного в натуральной степени: ( a : b ) n = a n : b n
Можно обобщить до: ( ( ( a n 1 ) n 2 ) … ) n k = a n 1 · n 2 · … · n k
6. Сравниваем степень с нулем:
7. Равенство a n b n будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.
8. Неравенство a m > a n будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.
Далее мы разберем каждое свойство подробно и попробуем привести доказательства.
Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:
Разберем конкретный пример, подтверждающий это.
Выполним необходимые математические действия: 2 2 · 2 3 = ( 2 · 2 ) · ( 2 · 2 · 2 ) = 4 · 8 = 32 и 2 5 = 2 · 2 · 2 · 2 · 2 = 32
Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:
a m − n · a n = a ( m − n ) + n = a m
Из него можно вывести: a m − n · a n = a m
Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π : π 5 : π 2 = π 5 − 3 = π 3
Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:
Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:
( a 1 · a 2 · … · a k ) n = a 1 n · a 2 n · … · a k n
Начнем сразу с примера: ( 5 2 ) 3 = 5 2 · 3 = 5 6
А теперь сформулируем цепочку равенств, которая докажет нам верность равенства:
a p q y s = a p · q · y · s
6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.
Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени a n с положительным основанием и натуральным показателем это будет верно.
Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.
Вспомним, как правильно умножать отрицательные числа: произведение a · a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда 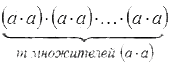
Тогда
7. Далее разберем следующее свойство, формулировка которого такова: из двух степеней, имеющих одинаковый натуральный показатель, больше та, основание которой больше (и наоборот).
8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.
Докажем эти утверждения.
Пример с конкретными числами: 3 7 > 3 2
Основные свойства степеней с целыми показателями
Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).
Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0 ) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:
1. a m · a n = a m + n
2. a m : a n = a m − n
3. ( a · b ) n = a n · b n
4. ( a : b ) n = a n : b n
Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.
Условия: p = 0 или натуральное число; q – аналогично.
( a 0 ) q = 1 q = 1 a 0 · q = a 0 = 1
Следовательно, ( a 0 ) q = a 0 · q
Для q = 0 все точно так же:
( a p ) 0 = 1 a p · 0 = a 0 = 1
Вспомним доказанное выше свойство частного в степени и запишем:
1 a p q = 1 q a p q
Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.
Тогда неравенство можно преобразовать следующим образом:
Запишем правую и левую части в виде разности и выполним необходимые преобразования:
Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.
Основные свойства степеней с рациональными показателями
В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:
Согласно тому, что из себя представляет степень с дробным показателем, получим:
Свойства корня позволят нам вывести равенства:
a m 1 · m 2 n 1 · n 2 · a m 2 · m 1 n 2 · n 1 = a m 1 · n 2 · a m 2 · n 1 n 1 · n 2
Из этого получаем: a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2
a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2
Показатель степени можно записать в виде:
m 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 · n 2 n 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 n 1 + m 2 n 2
Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
Доказательства остальных равенств:
a · b m n = ( a · b ) m n = a m · b m n = a m n · b m n = a m n · b m n ; ( a : b ) m n = ( a : b ) m n = a m : b m n = = a m n : b m n = a m n : b m n ; a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = = a m 1 m 2 n 1 n 2 = a m 1 · m 2 n 1 n 2 = = a m 1 · m 2 n 2 · n 1 = a m 1 · m 2 n 2 · n 1 = a m 1 n 1 · m 2 n 2
Используем свойство корней и выведем: a m n b m n
Рациональные числа p и q можно привести к общему знаменателю и получить дроби m 1 n и m 2 n
Их можно переписать в следующем виде:
a m 1 n a m 2 n a m 1 n > a m 2 n
Тогда можно сделать преобразования и получить в итоге:
a m 1 n a m 2 n a m 1 n > a m 2 n
Основные свойства степеней с иррациональными показателями
1. a p · a q = a p + q
2. a p : a q = a p − q
3. ( a · b ) p = a p · b p
4. ( a : b ) p = a p : b p
Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a > 0 обладают теми же свойствами.
Степень числа: определения, обозначение, примеры
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).
Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Степень числа с целым положительным показателем можно отобразить в виде формулы: 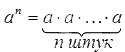
При этом n – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0
При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Проиллюстрируем нашу мысль конкретными примерами:
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как
При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
и так далее (при этом сами приближения являются рациональными числами).
Степень и ее свойства. Определение степени
Разделы: Математика
Ознакомить учащихся со свойствами степеней с натуральными показателями и научить выполнять действия со степенями.
Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а.
По определению степени:
а n =
Нахождение значения степени называют возведением в степень.
1. Примеры возведения в степень:
2. Представьте в виде квадрата числа: 25 ; 0,09 ;
25 = 5 2 ; 0,09 = ( 0,3 ) 2 ;
.
3. Представьте в виде куба числа:
4. Найти значения выражений:
а) 3• 10 3 = 3• 10• 10• 10 = 3• 1000 = 3000
1. Запишите произведение в виде степени:
б)
2. Представьте в виде квадрата числа:
16 ; 0,25 ; 
3. Представьте в виде куба числа:
125 ; 0,027 ; 
4. Найти значения выражений :
Для любого числа а и произвольных чисел m и n выполняется:
Правило: При умножении степеней с одинаковыми основаниями основания оставляют прежним, а показатели степеней складывают.
a m a n a k = a m + n a k = a ( m + n ) + k = a m + n + k
1. Представить в виде степени:
б) y• y 6 = y 1 • y 6 = y 1 + 6 = y 7
в) b 2 • b 5 • b 4 = b 2 + 5 + 4 = b 11
г) 3 4 • 9 = 3 4 • 3 2 = 3 6
д) 0,01• 0,1 3 = 0,1 2 • 0,1 3 = 0,1 5
2. Представить в виде степени и найти значение по таблице:
б) 3 2 • 3 5 = 3 7 = 2187
1. Представить в виде степени:
д) 2 3 •2 4 к) 0,3 3 •0,09
2. Представить в виде степени и найти значение по таблице:
б) 3 4 •3 2 г) 27• 243
Для любого числа а
по определению частного:
Правило: При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Определение: Степень числа а, не равного нулю, с нулевым показателем равна единице:
1. Представьте в виде степени частное:
г) с 5 :с 0 = с 5 :1 = с 5
2. Найдите значения выражений:
б) 10 20 :10 17 = 10 3 = 1000
в)
г)
д)
1. Представьте в виде степени частное:
2. Найдите значения выражений:
в)
г)
д)
Возведение в степень произведения.
Для любых а и b и произвольного натурального числа n:
По определению степени
( ab ) n =
Сгруппировав отдельно множители а и множители b, получим:

Доказанное свойство степени произведения распространяется на степень произведения трех и более множителей.
( a• b• c ) n = a n •b n •c n ;
Правило: При возведении в степень произведения возводят в эту степень каждый множитель и результат перемножают.
1. Возвести в степень:
б) (2• х• у ) 3 =2 3 •х 3 •у 3 = 8• х 3 •у 3
в) ( 3• а ) 4 = 3 4 •а 4 = 81• а 4
д) (-0,2• х• у ) 2 = (-0,2) 2 •х 2 •у 2 = 0,04• х 2 •у 2
е) (-3• a• b• c ) 4 = (-3) 4 •a 4 •b 4 •c 4 = 81• a 4 •b 4 •c 4
2. Найти значение выражения:
а) (2• 10) 4 = 2 4 •10 4 = 16• 1000 = 16000
б) (3• 5• 20) 2 = 3 2 •100 2 = 9• 10000= 90000
в) 2 4 •5 4 = (2• 5) 4 = 10 4 = 10000
г) 0,25 11 •4 11 = (0,25• 4) 11 = 1 11 = 1
д)
1. Возвести в степень:
е)
2. Найти значение выражения:
г)
д)
Возведение в степень степени.
Для любого числа а и произвольных натуральных чисел m и n:
По определению степени
( а m ) n =
Правило: При возведении степени в степень основание оставляют тем же, а показатели перемножают.
1. Возвести в степень:
( а 3 ) 2 = а 6 ( х 5 ) 4 = х 20
( у 5 ) 2 = у 10 ( b 3 ) 3 = b 9
2. Упростите выражения:
а) а 3 •( а 2 ) 5 = а 3 •а 10 = а 13
б) ( b 3 ) 2 •b 7 = b 6 •b 7 = b 13
в) ( х 3 ) 2 •( х 2 ) 4 = х 6 •х 8 = х 14
г) ( у• у 7 ) 3 = ( у 8 ) 3 = у 24
3. Найдите значение выражений:
а)
б)
1. Возвести в степень:
в) ( у 3 ) 2 г) ( b 4 ) 4
2. Упростите выражения:
3. Найдите значение выражений:
а)
б)
Приложение
1ю Запишите произведение в виде степени:
б)
2. Представьте в виде квадрата числа:
25 ; 0,16 ; 
3. Представьте в виде куба числа:
64 ; 0,125 ; 
4. Найти значения выражений:
1. Запишите произведение в виде степени:
б)
в) с• с• с• с• с• с• с• с• с
2. Представьте в виде квадрата числа: 100 ; 0,49 ; 
3. Представьте в виде куба числа:
1000 ; 0,008 ; 
4. Найти значения выражений :
1. Запишите произведение в виде степени:
б)
д) ( bс ) • ( bс ) • ( bс ) • ( bc )
2. Представьте в виде квадрата числа:
81 ; 0,64 ;
3. Представьте в виде куба числа:
216 ; 0,064 ; 
4. Найти значения выражений :
1. Представить в виде степени:
д) 2 2 •2 5 к) 0,2 3• 0,04
2. Представить в виде степени и найти значение по таблице:
1. Представить в виде степени:
д) 2 3 •2 6 к) 0,3 4 •0,27
2. Представить в виде степени и найти значение по таблице:
1. Представить в виде степени:
б) х 7 •х 8 ж) 3 4 •27
д) 2 4 •2 5 к) 0,2 2 •0,008
2. Представить в виде степени и найти значение по таблице:
1. Представьте в виде степени частное:
2. Найдите значения выражений:
в)
г)
д)
1. Представьте в виде степени частное:
2. Найдите значения выражений:
в)
г)
д)
1. Представьте в виде степени частное:
2. Найдите значения выражений:
в)
г)
д)
Возведение в степень произведения.
1. Возвести в степень:
2. Найти значение выражения:
д)
1. Возвести в степень:
е)
2. Найти значение выражения:
г)
1. Возвести в степень:
2. Найти значение выражения:
д)
Возведение в степень степени.
1. Возвести в степень:
2. Упростите выражения:
3. Найдите значение выражений:
а)
б)
1. Возвести в степень:
2. Упростите выражения:
3. Найдите значение выражений:
а)
б)
1. Возвести в степень:
2. Упростите выражения:
3. Найдите значение выражений:
а)
б)

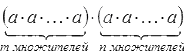
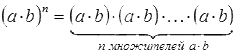
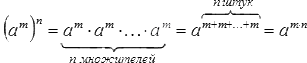
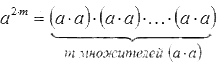
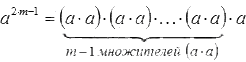


 .
.





































