Квадрат

Квадрат – прямоугольник с равными сторонами.
Квадрат – параллелограмм, у которого все стороны равны и все углы равны.
Свойства квадрата
Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.
Признаки квадрата
Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:
1. Все стороны равны и среди внутренних углов есть прямой угол.
2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.
Описанная окружность
Около квадрата можно описать окружность. Сторона и радиус
окружности связаны соотношением:
Вписанная окружность
В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением:
Площадь квадрата
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Определение квадрата 8 класс геометрия
Квадрат — прямоугольник, у которого все стороны равны (ромб, у которого углы прямые).
Из всех прямоугольников одного и того же периметра квaдрат имеет наибольшую площадь.
Из всех прямоугольников определенной площади квадрaт имеет наименьший периметр.
Слово «квaдрaт» происходит от латинского «gudratus» — четырехугольник.
Квадрaт был первым четырехугольником, который рассматривался в геометрии.
Любой квадрат можно разрезать на два равных квадрата.
Свойства и признаки квадрата
Свойства квадрата:
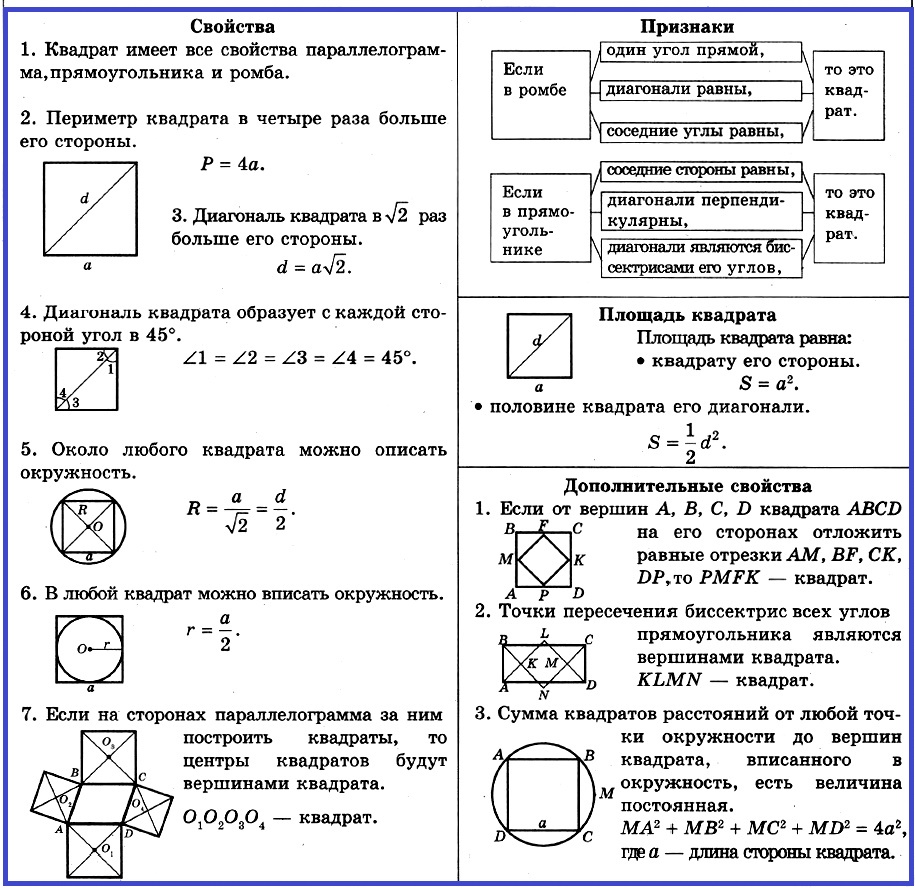
1. Квадрaт имеет все свойства параллелограмма, прямоугольника и ромба.
2. Периметр квадрата в четыре раза больше его стороны.
3. Диагональ квадрата в √2 раз больше его стороны.
4. Диагональ квадрата образует с каждой стороной угол в 45°.
5. Около любого квадрата можно описать окружность.
6. В любой квадрат можно вписать окружность.
7. Если на сторонах параллелограмма за ним построить квадраты, то центры квадратов будут вершинами квадрата.
Признаки квадрата:
Если в ромбе один угол прямой,
Если в ромбе диагонали равны,
Если в ромбе соседние углы равны,
Если в прямоугольнике соседние стороны равны,
Если в прямоугольнике диагонали перпендикулярны,
Если в прямоугольнике диагонали являются биссектрисами его углов.
Дополнительные свойства
1. Если от вершин А, В, С, D квадрата ABCD на его сторонах отложить равные отрезки AM, BF, СК, DP, то PMFK — квадрат.
2. Точки пересечения биссектрис всех углов прямоугольника являются вершинами квадрата.
3. Сумма квадратов расстояний от любой точки окружности до вершин квадрата, вписанного в окружность, есть величина постоянная.
Это конспект по теме «Квадрат и его свойства». Выберите дальнейшие действия:
Что такое квадрат: определение и свойства
В данной публикации мы рассмотрим определение и свойства (с рисунками) одной из основных геометрических фигур – квадрата.
Определение квадрата
Свойства квадрата
Свойство 1
Диагонали квадрата равны, расположены под прямым углом друг к другу, в точке пересечения делятся пополам.
Свойство 2
Диагонали квадрата являются биссектрисами его углов. Для рисунке выше:
Свойство 3
Центром описанной вокруг и вписанной в квадрат окружностей является точка пересечения его диагоналей (в нашем случае – E).
При этом радиусы окружностей можно вычислить через длину стороны или диагонали квадрата:
Также, один радиус можно выразить через другой:
Свойство 4
Зная длину стороны или диагонали квадрата, можно найти его площадь или периметр.
Периметр (P) квадрата через сторону:
P = a + a + a + a = 4 ⋅ a
Периметр (P) квадрата через диагональ:
Площадь (S) квадрата через сторону:
Площадь (S) квадрата через диагональ:
Квадрат
Квадрат — это четырехугольник, имеющий равные стороны и углы.
Диагональ квадрата — это отрезок, соединяющий две его противоположные вершины.
Параллелограмм, ромб и прямоугольник так же являются квадратом, если они имеют прямые углы, одинаковые длины сторон и диагоналей.
Свойства квадрата
1. Длины сторон квадрата равны.
2. Все углы квадрата прямые.
\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^
3. Противолежащие стороны квадрата параллельны друг другу.
AB \parallel CD, BC \parallel AD
4. Сумма всех углов квадрата равна 360 градусов.
\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^
5. Величина угла между диагональю и стороной равна 45 градусов.
\angle BAC = \angle BCA = \angle CAD = \angle ACD = 45^
6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
\angle AOB = \angle BOC = \angle COD = \angle AOD = 90^
Так как квадрат это прямоугольник \Rightarrow диагонали равны; так как — ромб \Rightarrow диагонали перпендикулярны. А так как — параллелограмм, \Rightarrow диагонали разделены точкой пересечения пополам.
7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.
\triangle ABD = \triangle CBD = \triangle ABC = \triangle ACD
8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.
\triangle AOB = \triangle BOC = \triangle COD = \triangle AOD
9. Если сторона квадрата равна a, то, диагональ будет равна a \sqrt <2>.
Отсюда: AC = \sqrt<2>\cdot a
10. Центром квадрата, а так же вписанной в него и описанной окружности является точка пересечения диагоналей
Конспект урока по теме»Квадрат» (8 класс)
Урок по геометрии в 8 классе
Цель : сформировать у учащихся знания о квадрате как последнем представителе четырехугольников, как частного случая параллелограмма, прямоугольника и ромба; создать условия на уроке для того, чтобы учащиеся самостоятельно перечислили все свойства квадрата, на основе ранее изученного и применяли их при решении задач.
— предметные: умение проводить классификацию, логические обоснования, доказательства математических утверждений; формирование умения построения математической модели решения задач;
— метапредметные: умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки; развивать логическое мышление, познавательную активность и навыки научной речи;
— личностные: создание педагогических условий для формирования у обучающихся положительной мотивации к учению, умения преодолевать посильные трудности, чувства коллективизма, взаимовыручки и уважения друг к другу, умения вести диалог, понимать смысл поставленной задачи; выстраивать аргументацию, приводить примеры.
Тип урока : открытие новых знаний.
Основные методы обучения: наглядный, практический, исследовательский, с элементами технологии деятельностного метода.
Формы организации учебной деятельности: фронтальная, групповая, индивидуальная, самостоятельная.
Техническое обеспечение урока: компьютер, проектор, документ-камера.
1 .Организационный этап.
Здравствуйте, дети! Садитесь!
Ну-ка проверь дружок,
Ты готов начать урок?
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ли внимательно глядят?
Каждый хочет получать,
Только лишь оценку пять.
2. Постановка цели и задач урока.
Сейчас вы послушаете стихотворение и сами определите тему и сформулируйте цели и задачи нашего урока.
Из него мы строим дом.
И окошко в доме том.
За него в обед садимся,
В час досуга веселимся.
Ему каждый в доме рад.
Вспомним, о чём мы с вами говорили на прошлых уроках? Какие фигуры мы изучили? А какую фигуру мы ещё не изучали? Какова же тема и цель нашего урока?
3. Актуализация знаний обучающихся.
Математического диктанта с взаимопроверкой.
1.Является ли прямоугольником параллелограмм, у которого есть прямой угол? (Обязательно ли является прямоугольником четырехугольник, у которого есть прямой угол?)
2. Верно ли, что каждый прямоугольник является параллелограммом? (Верно ли, что каждый параллелограмм является прямоугольником?)
3. Диагонали прямоугольника АЕKМ пересекаются в точке О. Отрезок АО = 3. Найдите длину диагонали ЕМ. (Диагонали параллелограмма равны 3 и 5 дм. Является ли этот параллелограмм прямоугольником?)
4. Диагонали четырехугольника равны. Обязательно ли этот четырехугольник является прямоугольником? (Сумма длин диагоналей прямоугольника 13 см. Найдите длину каждой диагонали.)
6.Верно ли, что каждый параллелограмм является ромбом? (Периметр ромба равен 30 см. Найдите его стороны.)
4. Открытие новых знаний.
На доске изображены фигуры: параллелограмм, прямоугольник и ромб. Ученики по очереди выходят к доске и рассказывают определение, свойства и признаки этих фигур.
А теперь посмотрим на квадрат. Назовите элементы этой фигуры.
— Сосчитайте, сколько у квадрата сторон?
— Что вы узнали о квадрате?
У квадрата 4 вершины, 4 стороны, 4 угла.
— Чем являются стороны квадрата? (отрезками)
Какие углы у квадрата? (прямые)
Измерьте стороны квадрата, сделайте вывод, (они равны)
Есть ли, что- то общего у квадрата с фигурами, изображёнными на доске?
А можно ли дать определение квадрата, используя данные фигуры?
1ряд – определение через параллелограмм и запишет все свойства квадрата, которые он взял от параллелограмма
2ряд – определение через прямоугольник и запишет все свойства квадрата, которые он взял от прямоугольника
3ряд–определение через ромб и запишет все свойства квадрата, которые он взял от ромба
Итог: выступление групп, подведение итога. Все результаты выступлений записываются на доске и в тетрадях.
5. Первичное закрепление материала
Физкультминутка для глаз, (закрыли глаза крепко, затем открыли. Так повторили несколько раз. Круговые движения глаз вправо, влево. Закрыли спокойно глаза, немного отдохнули.)
№ 412 из учебника Л. С. Атанасян (разобрать решение этой задачи с использованием документ-камеры).

1.треугольник АВС – прямоугольный и равнобедренный 

2.треугольник АFE – прямоугольный.


3.треугольник DВЕ – прямоугольный.


4. С D Е F – квадрат С D = DE = EF = CF.
8.Рефлексия. Подведение итогов.
Итог : С какой геометрической фигурой мы работали на уроке?
— Какие условия должны выполняться, чтобы фигура была квадратом?
— Теперь оцените свою работу сами. Поднимите руку, кто работал «на отлично». Нарисуйте в тетради восклицательный знак.
— Поднимите руку, кто оценил работу на уроке как «хорошую». Нарисуйте в тетради вопросительный знак.
— Поднимите руку, кто оценил работу на уроке как «неудовлетворительную». Нарисуйте в тетради число ноль
.- Что у вас не получилось на уроке? Что было непонятно?
9. Домашнее задание
Выучить теоретический материал, п.45
Решить по учебнику №410,411.
Творческое задание. Сделать презентацию. Доказать, что квадрат – это идеальный четырёхугольник и где в жизни встречается нам квадрат?













.png)




