интегральная сумма римана определение

Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций

После обобщения выражения и определения получили, что любая непрерывная функция y = f ( x ) с числом I имеет отрезок, который и получил название определенного интеграла.

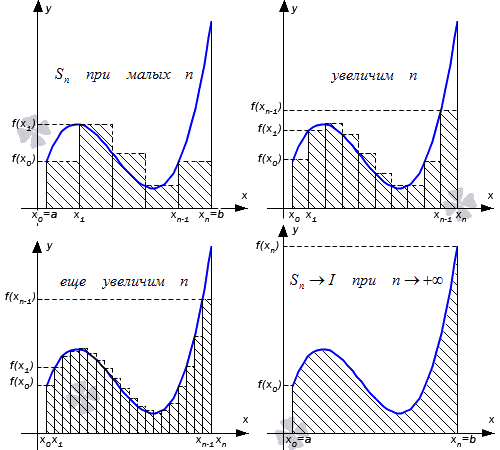
Его геометрическое понятие было показано в школе в 11 классе. Рассмотрим рисунок, приведенный ниже. Имеем изображение определенного интеграла.

В данной статье будет показано определения определенного интеграла, которые были заданы Риманом и Дарбу, Ньютоном-Лейбницом. Подробно будет показано условие интегрируемости функции на заданном определенном отрезке с перечислением интегрируемых функций.

Определенный интеграл Римана

Рассмотрим рисунок, приведенный ниже.

Числа a и b называют нижним и верхним пределом интегрирования, а f ( x ) – подынтегральная функция, где x – переменная интегрирования.

Определенный интеграл Дарбу

Чтобы понять необходимо и достаточное условие существования определенного интеграла Дарбу, необходимо применить несколько определений.

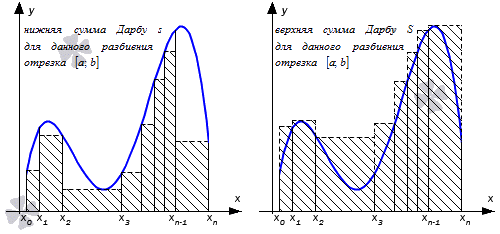
для разбиения отрезка [ a ; b ] называют нижней и верхней суммами Дарбу.

Рассмотрим рисунок, приведенный ниже.

Определенный интеграл Ньютона-Лейбница

Рассмотрим подробно понятие определенного интеграла Ньютона-Лейбница.

Необходимое условие интегрируемости функции на отрезке, виды интегрируемых функций

Рассмотрим необходимое условие существования определенного интеграла функции на отрезке.

Виды функций, для которых существует определенный интеграл:

Рассмотрим рисунок, приведенный ниже. На нем располагается пример интегрируемой функции.

Итоги

Задавание определенного интеграла Римана происходит через предел интегральных сумм, а интеграл Дарбу – предел разности верхних и нижних сумм Дарбу, в свою очередь интеграл Ньютона-Лейбница – при помощи значения первообразной.

Источник

Интеграл Римана

Определение интеграла Римана

\exists\delta>0 \colon \forall(P_<[a,b]>,\xi_P)

Сама функция при этом называется интегрируемой по Риману на сегменте а класс всех таких функций будем обозначать символом Очевидно, что если то она ограничена на этом сегменте.

Верхним и нижним интегралами Дарбу ограниченной функции называются соответственно числа:

Теорема 1. Если интеграл Римана и определённый интеграл Ньютона-Лейбница функции существуют одновременно, то они равны друг другу.

Теорема 2. Для ограниченной функции интегралы Римана и Дарбу эквивалентны, то есть они существуют или не существуют одновременно, а в случае существования их значения совпадают.

Для интеграла Римана (Дарбу) используют то же обозначение, что и для интеграла Ньютона-Лейбница

Теорема 3. Пусть ограниченная функция и — множество точек разрыва. Функция интегрируема по Риману на тогда и только тогда, когда — множество лебеговой меры 0.

Теорема 5 (основная формула интегрального исчисления). Если множество точек разрыва функции = не более чем счётно, то функция является первообразной в широком смысле для и имеет место формула Ньютона-Лейбница

Пусть и функции дифференцируемы на Тогда

Пусть — дифференцируемая функция и Тогда имеет место равенство

которое называется формулой замены переменной в интеграле Римана.

Пусть — дифференцируемые функции, Тогда и выполняется равенство

которое называется формулой интегрирования по частям.

Если — ограниченная функция и то определим интеграл Римана от функции на множестве как

Если граница ограниченного множество имеет лебегову меру 0, то это множество называется измеримым по Жордану, а интеграл

Применение интеграла Римана

Применение интеграла Римана чаще всего проводится по одной и той же схеме, к которой приводят рассуждение геометрического или физического характера.

Теорема 1 (связь АФП с интегралом Римана). Если для АФП существует такая интегрируемая по Риману функция что выполняются соотношения

Эта теорема даёт возможность свести задачи вычисления площади плоской фигуры, объёма тела вращения, длины дуги кривой, статических моментов и моментов инерции кривых относительно фиксированных прямых, а также ряд других задач геометрического или физического содержания к задаче интегрирования соответствующих функций по Риману.

Поскольку применение обычного интеграла Римана (или, как ещё говорят, однократного интеграла) для вычисления различных моментов, координат центра тяжести и т.п. представляется нерациональным, то ниже приведём только схемы и методы вычисления геометрических величин, которые достаточно просто и рационально находить именно с использованием интеграла Римана.

и площадь криволинейной трапеции вычисляется по формуле

2. Площадь криволинейного сектора. Криволинейным сектором в полярной системе координат называется множество

Площадь криволинейного сектора вычисляется по формуле

5. Длина дуги гладкой кривой. Множество называется простой гладкой кривой (траекторией), если существует отображение

Если то последняя формула приобретает вид

8. Объем тела, полученный вращением сектора вокруг полярной оси, равен

Источник

Определение и свойства кратного интеграла Римана

Разбиения.

Пусть множество $G$ измеримо по Жордану в $\boldsymbol>$. Совокупность измеримых по Жордану в $\boldsymbol>$ и попарно непересекающихся множеств $G_<1>, \ldots, G_$ называется разбиением $G$, если $G = \displaystyle\bigcup_^ G_i$. Разбиение будем обозначать буквой $T$.

Пусть $d(G_)$ есть диаметр множества $G_$, то есть
$$
d(G_) = \sup_, y \in G_> \rho (x, y).\nonumber
$$

Число $l(T) = \displaystyle\max_<\overline<1, N>> d(G_)$ будем называть мелкостью разбиения $T$.

Разбиение $T = \\>$, $i = \overline<1, N>$, будем называть продолжением разбиения $T’ = \\>$, $i = \overline<1, N>$, и писать $T \prec T’$, если каждое из множеств $G_$ является подмножеством некоторого множества $G’_$. Очевидно, что из $T \prec T’$ следует, что $l(T) \leq l(T’)$.

Интегральные суммы Римана. Суммы Дарбу.

Пусть функция $f(x)$ определена на измеримом по Жордану множестве $G$, а $T$ есть разбиение множества $G: T = \\>, i = \overline<1, N>$. Возьмем в каждом из множеств $G_$ по точке $\xi_$. Выражение
$$
\sigma_ (f, \xi, G) = \sum_^ f(\xi_)m(G_)\nonumber
$$
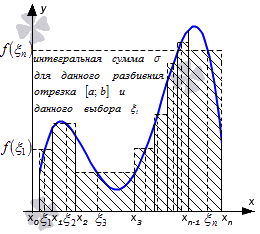
называется интегральной суммой Римана функции $f(x)$ на множестве $G$, соответствующей разбиению $T$ и выборке $\xi = (\xi_<1>, \ldots, \xi_)$. Иногда для краткости будем обозначать сумму Римана просто через $\sigma_$.

Если функция $f(x)$ ограничена на множестве $G$, то для любого разбиения $T = \\>$, $i = \overline<1, N>$, определены числа
$$
m_ = \inf_> f(x),\quad M_ = \sup_> f(x).\nonumber
$$

Выражения
$$
S_ = \sum_^M_m(G_),\quad s_ = \sum_^m_m(G_)\label
$$
называются верхней и нижней суммами Дарбу, соответствующими разбиению $T$.

Интеграл Римана как предел интегральной суммы.

Число $I$ называется пределом интегральной суммы $\sigma_$ при мелкости разбиения $l(T) \rightarrow 0$, если для любого $\varepsilon > 0$ найдется $\delta > 0$ такое, что для любого разбиения $T$ с мелкостью $l(T) Теорема 1.

(критерий интегрируемости)

Для того чтобы ограниченная функция \(f(x)$ была интегрируема на измеримом по Жордану множестве $G \in \boldsymbol>$, необходимо и достаточно, чтобы для любого $\varepsilon > 0$ нашлось такое $\delta > 0$, что для любого разбиения $T$ с мелкостью $l(T) Доказательство.

Доказательство теоремы 1 ничем не отличается от соответствующего доказательства для определенного интеграла.

Справедлива более сильная теорема. Но для ее доказательства сформулируем несколько вспомогательных лемм.

Если измеримые множества \(G$ и $\Omega$, принадлежат пространству $\boldsymbol>$ и $m(\Omega) 0$ такое, что для любого разбиения $T$ множества $G$ с мелкостью $l(T) Доказательство.

\(\circ$ Поскольку измеримое множество $\Omega$, мера которого меньше $\varepsilon$, содержится в клеточном множестве, мера которого меньше, чем 2$\varepsilon$, а клеточное множество состоит из конечного числа клеток, то достаточно доказать лемму для случая, когда множество $\Omega$ есть клетка $\Pi$. Ограничимся случаем клетки в $\boldsymbol>$. Построим для прямоугольника $\Pi$ рамку (рис. 46.1).

Рис. 46.1

Можно так подобрать $\delta$, что площадь прямоугольника $\Pi_<\delta>$, получающегося из $\Pi$ добавлением рамки, не будет превышать 2$\varepsilon$. Если мелкость разбиения множества $G$ меньше $\delta$, то все элементы разбиения $G_$ имеющие непустое пересечение с $\Pi$, лежат в прямоугольнике $\Pi_<\delta>$, и, следовательно, сумма их мер не превышает меры $\Pi_<\delta>$. $\bullet$

Если $\Omega_<1>$ и $\Omega_<2>$ — непересекающиеся замкнутые множества в $\boldsymbol>$ и хотя бы одно из этих двух множеств ограничено, то $\rho(\Omega_<1>, \Omega_<2>) > 0$.

Если $\rho(\Omega_<1>, \Omega_<2>) = \delta > 0$, множество $G \subset \Omega_ <1>\cup \Omega_<2>$ и диаметр множества $G$ меньше $\delta$, то либо $G \subset \Omega_<1>$, либо $G \subset \Omega_<2>$.

Теперь перейдем к формулировке и доказательству теоремы.

Для того чтобы функция $f(x)$, ограниченная на измеримом по Жордану множестве $G \in \boldsymbol>$, была интегрируемой на множестве $G$, необходимо и достаточно, чтобы для любого $\varepsilon > 0$ нашлось такое разбиение $T$ множества $G$, что $S_-s_ Доказательство.

\(\circ$ Необходимость следует из теоремы 1.

Достаточность. Пусть $|f(x)| 0$ нашлось разбиение $T_<0>$ множества $G$, для которого разность сумм Дарбу меньше $\varepsilon /2$. Без ограничения общности можно считать, что $T_ <0>= \^<0>, \tilde_<1>^<0>, \ldots, G_

^<0>, \tilde_

^<0>\>$, где множества $G_^<0>$ являются компактами, а сумма мер множеств $\<\tilde_<1>^<0>, \ldots, \tilde_

^<0>\>$ не превышает $\varepsilon /(8M)$. Это следует из того, что в каждое измеримое множество можно вложить компакт, сколь угодно мало отличающийся от этого множества по мере (это свойство доказано здесь), а при измельчении разбиения разность сумм Дарбу может только уменьшиться.

Обозначим объединение множеств $\tilde_^<0>$ через $A$. В силу леммы 2 существует число $\delta > 0$ такое, что расстояние между любыми двумя компактами $G_^<0>$ превышает $\delta$. Пусть $T$ — произвольное разбиение множества $G$ с мелкостью, не превышающей $\delta$. В силу леммы 3 множества, составляющие это разбиение, можно разделить на две группы. Множества, входящие в первую группу, целиком лежат в одном из множеств $G_^<0>$, а множества, входящие во вторую группу, имеют непустое пересечение со множеством $A$. В силу леммы 1 сумма мер множеств второй группы не превышает $\varepsilon /(2M)$. Та часть суммы $S_-s_$, которая соответствует первой группе, не превышает $\varepsilon /2$, поскольку при измельчении разбиения разность сумм Дарбу не увеличивается, а часть, соответствующая второй группе, не превышает $\varepsilon /2$ в силу того, что $|f(x)|

Классы интегрируемых функций.

Непрерывная на измеримом по Жордану компакте функция \(f(x)$ интегрируема на этом компакте.

Напомним, что компакт в $\boldsymbol>$ — это ограниченное и замкнутое множество и что функция $f(x)$, непрерывная на компакте, равномерно непрерывна на этом компакте (теорема Кантора).

Доказательство теоремы 3 ничем не отличается от соответствующего доказательства теоремы об интегрируемости функции одной переменной, непрерывной на отрезке.

Докажем более общую теорему.

Пусть функция $f(x)$ ограничена на измеримом компакте $G \subset \boldsymbol>$ и множество ее точек разрыва имеет жорданову меру нуль. Тогда функция $f(x)$ интегрируема на $G$.

$\circ$ Пусть $E$ есть множество точек разрыва функции $f(x)$ и $m(E) = 0$. Тогда для любого $\varepsilon > 0$ найдется такое открытое измеримое множество $A$, что $E \subset A$ и
$$
m(A) 0\) найдется разбиение $\, \ldots, G_\> = T’$ множества $G \backslash A$ такое, что
$$
S_-s_ = \sum_^ (M_-m_)m(G_) Замечание.

В условиях теоремы 4 можно отказаться от требования, чтобы измеримое множество $G$ было компактом. Согласно критерию измеримости множества измеримое множество $G$ ограничено и $m(\partial G) = 0$. Так как $G$ и $\partial G$ — измеримые множества, то замкнутое множество $\overline = G \cup\partial G$ измеримо по Жордану, то есть $\overline$ — измеримый компакт в $\boldsymbol>$. Если доопределить функцию $f(x)$ нулем на $\partial G$, то она останется ограниченной, а множество ее точек разрыва будет иметь жорданову меру нуль, так как оно содержится во множестве $E \cup \partial G$ меры нуль. В силу теоремы 4 функция $f(x)$ интегрируема на множестве $\overline$, а следовательно, и на измеримом подмножестве $G$.

Свойства кратного интеграла.

Поскольку все перечисленные свойства доказываются так же, как и соответствующие свойства определенного интеграла, то большая часть этих свойств не будет обосновываться подробными доказательствами.

Справедливо равенство $\displaystyle\int\limits_G 1 \cdot dx = m(G)$.

$\circ$ Для любого разбиения $T$ выполнено равенство
$$
\sigma_(1, \xi, G) = \sum_^ m(G_) = m(G).\ \bullet\nonumber
$$

Если $f(x) > 0$ и $f(x)$ — интегрируемая на измеримом по Жордану множестве $G$ функция, то $\displaystyle\int\limits_G f(x)\ dx \geq 0$.

Если $f_<1>(x)$ и $f_<2>(x)$ — интегрируемые на множестве $G$ функции, а $\alpha$ и $\beta$ — произвольные вещественные числа, то и функция $\alpha f_<1>(x) + \beta f_<2>(x)$ интегрируема на $G$, причем
$$
\int\limits_G (\alpha f_<1>(x) + \beta f_<2>(x))\ dx = \alpha \int\limits_G f_<1>(x)\ dx + \beta \int\limits_G f_<2>(x)\ dx.\nonumber
$$

Если $f_<1>(x)$ и $f_<2>(x)$ — интегрируемые на множестве $G$ функции и $f_<1>(x) \leq f_<2>(x)$ при $x \in G$, то
$$
\int\limits_G f_<1>(x)\ dx \leq \int\limits_G f_<2>(x)\ dx.\nonumber
$$

Если функция $f(x)$ непрерывна на измеримом связном компакте $G$, то найдется точка $\xi \in G$ такая, что
$$
\int\limits_G f(x)\ dx = f(\xi)m(G).\label
$$

$\circ$ Если $m(G) = 0$, то равенство \eqref очевидно. Пусть $m(G) > 0$, $\mu = \displaystyle\min_ f$, $M = \displaystyle\max_ f$. Тогда $\mu \leq f(x) \leq M$ при $x \in G$, $\mu m(G) \leq \displaystyle\int\limits_G f(x)\ dx \leq M m(G)$.Следовательно,
$$
\mu \leq \frac<1> \int\limits_G f(x)\ dx \leq M.\nonumber
$$Функция, непрерывная на связном множестве и принимающая на нем значения $\mu$ и $M$, принимает и все промежуточные значения, а поэтому существует точка $\xi \in G$ такая, что
$$
f(\xi) = \frac<1> \int\limits_G f(x)\ dx.\ \bullet\nonumber
$$

Если $\\>$, $k = \overline<1, m>$, есть разбиение множества $G$, то функция $f(x)$ интегрируема на множестве $G$ в том и только том случае, когда она интегрируема на каждом из множеств $G_$, причем
$$
\int\limits_G f(x)\ dx = \sum_ <\substack>^<\substack> \int\limits_> f(x)\ dx.\label
$$

Говорят, что формула \eqref выражает свойство конечной аддитивности интеграла по области интегрирования.

Произведение интегрируемых на измеримом множестве $G$ функций есть интегрируемая на множестве $G$ функция.

Если функция $f(x)$ интегрируема на измеримом множестве $G$, то функция $|f(x)|$ также интегрируема и
$$
\left|\int\limits_G f(x)\ dx\right| = \int\limits_G |f(x)|\ dx.\label
$$

В дальнейшем будем часто пользоваться свойством кратного интеграла, выраженным в следующей лемме.

Пусть функция $f(x)$ ограничена на измеримом по Жордану множестве $G$, а $E$ есть множество жордановой меры нуль. Если для любого разбиения $T = \\>$, $k = \overline<1, N>$, отбрасывать в интегральной сумме $\sigma_$ слагаемые, соответствующие тем множествам $G_$, которые имеют непустое пересечение с $E$, то это не повлияет ни на существование предела интегральной суммы при мелкости $l(T) \rightarrow 0$, ни на величину этого предела.

$\circ$ Если $m(G) = 0$, то лемма, очевидно, справедлива, так как для любого разбиения $\sigma_ = 0$. Пусть $m(G) > 0$ и $|f(x)| \leq c_<0>$ на множестве $G$. Для любого $\varepsilon > 0$ найдется клеточное множество $A$ такое, что $m(A) \leq \displaystyle\frac<\varepsilon><4c_<0>>$ и $E \subset A$. Будем множества разбиения $T$ нумеровать таким образом, чтобы $G_<1>, \ldots, G_$ имели непустое пересечение с $A$, a $G_, \ldots, G_$ не пересекались с $A$. В силу леммы 1 найдется такое $\delta > 0$, что при $l(T)

Достаточное условие измеримости множества в R n по Жордану.

Пусть \(G$ — измеримое множество в $\boldsymbol>$. Тогда цилиндр
$$
G_ = \<(x_<1>, \ldots, x_, x_): (x_<1>, \ldots, x_) \in G,\ 0 \leq x_ \leq h\>\nonumber
$$
есть измеримое множество в $\boldsymbol>$ и $m(G_) = hm(G)$.

$\circ$ Так как основание $G$ есть измеримое множество в $\boldsymbol>$, то для любого $\varepsilon > 0$ найдутся клеточные множества $A$ и $B$ такие, что
$$
A \subset G \subset B,\ m(B)-m(A) Теорема 5.

Пусть $G$ — измеримое множество в $\boldsymbol>$ и функция $f(x)$ интегрируема на $G$. Тогда график функции $f(x)$ имеет в $\boldsymbol>$ жорданову меру нуль.

$\circ$ Так как функция $f(x)$ интегрируема на множестве $G$, то для любого $\varepsilon > 0$ найдется разбиение $T = \\>$, $i = \overline<1, N>$, множества $G$ такое, что
$$
S_-s_ = \sum_^(M_-m_)m(G_) Следствие.

Если функция $f(x)$ непрерывна на измеримом компакте в $\boldsymbol>$, то ее график в $\boldsymbol>$ имеет жорданову меру нуль. Если граница области состоит из конечного объединения таких графиков, то область измерима по Жордану.

Источник

Определение интеграла Римана, простейшие свойства

Определение:

Пусть есть отрезок [math]\left [ a,b \right ][/math] и некоторое [math] \tau : a = x_0 \lt x_1 \lt \dots \lt x_n = b [/math] ( [math]\tau[/math] называется разбиением отрезка [math]\left [ a,b \right ][/math] ).

Определение:

[math]\Delta_k=x_-x_k[/math] длина текущего отрезка разбиения.

Определение:

[math]\operatorname \tau = \max \left \ < \Delta_0, \Delta_1, \dots, \Delta_\right \>[/math]

Тогда [math]\sigma \left ( f, \tau, \left \ < \overline\right \> \right )[/math] (также обозначается как [math]\sigma \left ( f, \tau \right )[/math] или [math]\sigma \left ( \tau \right )[/math] ) [math]

= \sum\limits_^[/math] [math]f \left ( \overline \right )\cdot\Delta_[/math]

Определение:

Определённым интегралом Римана функции [math]f[/math] называется предел её интегральных сумм, коротко записывается как [math]\int\limits_a^b f(x)\,dx = \int\limits_a^b f[/math]

Факт существования интеграла функции [math]f[/math] обозначается как [math]f \in \mathcal\left ( a,b \right )[/math]

Пусть [math]\exists I=\lim \sigma \left ( f, \tau \right ),

Источник

СОДЕРЖАНИЕ

Определение

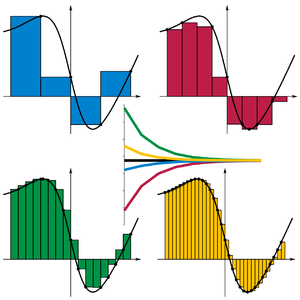
Некоторые особые виды сумм Римана

Методы

Тогда точки в разделе будут

Левая сумма Римана

Правая сумма Римана

Здесь f аппроксимируется значением в правой конечной точке. Это дает несколько прямоугольников с основанием Δ x и высотой f ( a + i Δ x ). Выполнение этого для i = 1,…, n и сложение результирующих областей дает

Правило средней точки

Ошибка этой формулы будет

Трапециевидная линейка

В этом случае значения функции f на интервале аппроксимируются средним значением значений на левой и правой конечных точках. Таким же образом, как и выше, простой расчет с использованием формулы площади

Ошибка этой формулы будет

Приближение, полученное с помощью правила трапеций для функции, такое же, как среднее значение левой и правой сумм этой функции.

Связь с интеграцией

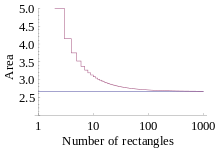
Для домена конечного размера, если максимальный размер элемента раздела уменьшается до нуля, это означает, что количество элементов раздела стремится к бесконечности. Для конечных разбиений суммы Римана всегда являются приближениями к предельному значению, и это приближение становится лучше по мере того, как разбиение становится более точным. Следующие анимации помогают продемонстрировать, как увеличение количества разделов (при уменьшении максимального размера элемента раздела) лучше соответствует «площади» под кривой:

Поскольку здесь предполагается, что красная функция является гладкой функцией, все три суммы Римана сходятся к одному и тому же значению, когда количество разбиений стремится к бесконечности.

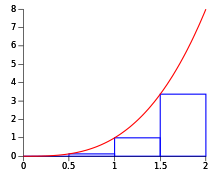
Пример

Например, площадь под кривой y = x 2 между 0 и 2 может быть вычислена процедурно с использованием метода Римана.

Если рассматривать предел как n → ∞, можно сделать вывод, что приближение приближается к фактическому значению площади под кривой по мере увеличения количества прямоугольников. Следовательно:

Этот метод согласуется с определенным интегралом, вычисленным более механическими способами:

В примере функции есть простая для поиска антипроизводная, поэтому оценка интеграла с помощью сумм Римана в основном является академическим упражнением; однако следует помнить, что не все функции имеют антипроизводные, поэтому оценка их интегралов путем суммирования практически важна.

Высшие измерения

Основная идея, лежащая в основе суммы Римана, состоит в том, чтобы «разбить» область посредством разделения на части, умножить «размер» каждой части на некоторое значение, которое функция принимает для этой части, и просуммировать все эти продукты. Это можно обобщить, чтобы можно было использовать суммы Римана для функций в областях более чем одного измерения.

Хотя интуитивно процесс разделения домена прост для понимания, технические детали того, как домен может быть разделен, становятся намного сложнее, чем в одномерном случае, и включают аспекты геометрической формы домена.

Два измерения

Три измерения

Произвольное количество измерений

Суммы Римана с более высокой размерностью следуют тому же принципу, что и от одного до двух или трех измерений. Для произвольной размерности n сумма Римана может быть записана как

Обобщение

В общих чертах суммы Римана можно записать

Источник